ADVERTISEMENTS:
In this article we will discuss about the Importance of Statistics in Education.
Definitions of Statistics:
“Statistics comprises the collection, tabulation, presentation and analysis of an aggregate of the facts, collected in methodical manner, without bias and related to predetermined purpose.” – Sutcliffe
The word “statistics” is derived from the Latin word “status”, which means political condition or status. Hence, it follows that the method of enumeration by which a state,’ condition is known called statistics. And is reality it is through statistics that we find out a state, population and its various sources of income and expenditure.
ADVERTISEMENTS:
According to Prof. A.L. Bowley:
“Statistics may be called the science of counting.”
According to Boddington:
“Statistics is the science of estimates and probabilities.”
ADVERTISEMENTS:
According to Lovitt:
“Statistics is the science which deals with the collection, classification and tabulation of numerical facts as the basis for explanation, description and comparison of phenomena.”
Tate, M.N. is statistics in Education (1953) has very beautifully summed up the concept of statistics as It’s all perfectly clear; you complete statistics (means, medians, modes etc.) from statistics (numerical facts) by statistics (statistics as a science or methodology).
Need, Importance and Uses of Statistics:
1. Group Comparison:
The achievements of a class are not uniform in every subject. It is found that one class is progressing faster is one subject, while another is progressing is a different one. Even the various sections of a particular class do not progress uniformly.
2. Individual Comparison:
Statistics helps in the individual comparison of students differing in respect of their ages, abilities and intelligence levels. It is statistics which tells us why thus students who are similar in every other respect yet do not show similar achievement is one particular subject.
3. Educational and Vocational Guidance:
Every individual student differs from others in his intellectual ability, interests, attitude and mental abilities students are given educational and vocational guidance so that they make the best use of these abilities and the process of guidance is based upon statistics only.
ADVERTISEMENTS:
4. Educational Experiments and Research:
With a change in place, line and circumstances, the aims, curricula and methods of education keep on changing. The work of research and experimentation cannot become reliable and valid without the use of statistics.
5. Essential for Professional Efficiency:
The teacher’s responsibility does not end when he teaches a particular subject in the classroom. His responsibility includes teaching the students, obtaining the desired level of knowledge for himself and assessing the achievement of modification in behaviour also.
6. Basis of Scientific Approach to Problems:
Statistics forms the basis of scientific approach to problems of Educational Psychology.
Meaning of Graphical Representation of Data:
A graphic representation is the geometrical image of a set of data. It is a mathematical picture. It enables us to think about a statistical problem in visual terms. A picture is said to be more effective than words for describing a particular thing or phenomenon.
Consequently the graphic representation of data proves quite an effective and an economic device for the presentation, understanding and inter predation of the collected statistical data. The statistical data can be represented by diagram, charts etc., so that the significance attached to these data may immediately be grasped, of course, the diagrams should be neatly and accurately drawn.
Advantages of Graphical Representation of Data:
1. The data can be presented in a more attractive and an appealing form.
2. It provides a more lasting effect on the brain. It is possible to have an immediate and a meaning group of large amounts of data through such presentation.
3. Comparative analysis and interpretation may be effectively and easily made.
4. Various valuable statistics like median, mode, quartiles may be easily computed. Through such representation, we also get an indication of correlation between two variables.
5. Such representation may help in the proper estimation evaluation and interpretation of the characteristics of items and individuals.
6. The real value of graphical representation use in us economy and effectiveness. It carries a lot of communication power.
7. Graphical representation helps in for-casting, as it indicates the trend of the data in the past.
Modes of Graphical Representation of Data:
We know that the data in the form of raw scores is known as ungrouped data and when it is organised into a frequency distribution, then it is referred to as grouped data. Separate methods are used to represent, these two types of data-ungrouped and grouped. Let us discuss them under separate heads.
Graphical Representation of Ungrouped Data:
For the ungrouped data (data not grouped into a frequency distribution) we usually make use of the following graphical representation:
1. Bar graphs or Bar diagrams.
2. Circle graph or Pie diagrams.
3. Pictograms.
4. Line graphs.
Bar Graph or Bar Diagram:
In bar graphs or diagrams, the data is represented by bars. Generally these diagrams or pictures are drawn on graph paper. Therefore these bar diagrams are also referred to as bar graphs.
These diagrams or graphs are usually available in two forms, vertical and horizontal. In the construction of both these forms, the lengths of the bars are in proportion to the amount of variables or traits (height, intelligence, number of individual, cost and so on) possessed. The width of the bars is not governed by any set of rules. It is an arbitrary factor. Regarding the space between two bars, it is conventional to have a space about one half of the width of a bar.
The data capable of representation through bar diagrams may be in the form of raw scores, total scores or frequencies, computed statistics and summarized figures like percentages and averages. Let us now try to illustrate the task of drawing the bar-graph.
Example 1:
The following data was collected about the strength of students of Govt. Boys’ Intermediate College, Bijnor:
Represent the above data through a bar graph.
Solution:
Bar graph of the data given in Ex. 1.
The task of drawing the bar-graph may be further 10.4 shown by the help of following example:
Example 2:
120 class XII students of a school were asked to open for different work experiences.
The details of these options are given in table:
Represent the above data through a bar graph.
Solution:
The bar graph of the data given in Ex.2, can be depicted as in fig. 2.
Circle Graph, Pie diagram:
In this form of graphical representation, the data is presented through the sections or portions of a circle. The name pie-diagram is given to a circle diagram because in determining the circumference of a circle, we have to take into consideration, a quantity known as ‘pie’ (written as pie ‘π’).
Method of Construction:
The surface area of a circle is known to cover 22 or 360°. The data to be represented through a circle diagram may therefore be presented through 360°] parts or sections of a circle.
The total frequencies or value is equated to 360° and then the angles corresponding to component parts are calculated or the component parts are expressed as percentage of the total and then multiplied by 360/100 or 3.6, after determining these angles, the required sections in the circle are drawn.
For illustration, let us take the data given in previous example:
The numerical data may be converted into angles of a circle as in Fig. 3.
Figure 3. Representation of data through the pie-diagram-Area of work expiated for by students of class XII:
Picto-gram:
Numerical data of statistics may be represented by means of a picto-gram. Such representation may be shown by the help of Fig. 4.
Note:
Each students represents a strength of 100.
Line-Graphs:
Line graphs are simple mathematical graphs that are drawn on the graph paper by plotting the data concerning one variable on the horizontal x-axis and other variable of data on the vertical y-axis with the help of such graphs, the effect of one variable upon another variable during an experimental or a normative study, may be clearly demonstrated.
The construction of these graphs can be understood through the following example:
Example 3:
An intelligence test was administered on a student of class XI to demonstrate the effect of practice on learning.
The data so obtained may be studied from the following table:
Draw a line graph for the representation and interpretation of the above data.
Solution:
The line graph for the data given in Ex.3. can be drawn as in Fig. 5.
Graphical Representation of Grouped Data:
Frequency Distribution:
There are four methods of representing a frequency distribution on graphically:
1. The histogram.
2. The frequency polygon.
3. The cumulative frequency graph.
4. The cumulative frequency percentage curve or ogive.
These methods have been discussed one by one.
Histogram:
A histogram or column diagram is essentially a bar graph of a frequency distribution. The following points are to be kept in mind while constructing the histogram for a frequency distribution.
For example purposes, we can use the frequency dis given in Table 2:
1. The scores in the form of actual class limits as 19.5-24.5; 24.5-29.5 and soon are taken as examples in the construction of histogram, rather than the written class limits as 20 – 24; 25 – 30 and so on.
2. It is customary to take two extra intervals (classes) one below and the other above the given grouped intervals or classes (with zero frequency). In the case of frequency distribution given in Table 1, we can take 14.5-19.5 and 69.5 – 74.5 as the required class intervals.
3. Now we take the actual lower limits of all the class intervals (including the extra intervals) and try to plot them on the x-axis. The lower limit of the lowest interval (one of the extra intervals is taken at the intersecting point of x-axis and y-axis.
4. Frequencies of the distribution are plotted on the y-axis.
5. Each class or class interval with its specific frequency is represented by a separate rectangle. The base of each rectangle is the width of the class-interval (1) and the height is the respective frequency of that class or interval.
6. It is not essential to project the sides of the rectangle down to the base line.
7. Care should be taken to select the appropriate units of representation along the x-axis and the y-axis.
Both the x-axis and the y-axis should not be too short or too long.
A good general rule for this purpose as suggested by Garrett (1971) is:
To select x and y units which will make the height of the figure approximately 75% of its width.
The above procedure may be properly understood through fig. 6 which shows the histogram of the frequency dis given in Table 1:
Frequency Polygon:
A frequency polygon, as shown in fig. is essentially a line graph for the graphical representation of the frequency distribution. We can get a frequency polygon from a histogram, if the mid points of the upper bases of the rectangles are connected by straight lines. But it is not essential to plot a histogram prior to drawing a frequency polygon. We can construct it directly from a given frequency distribution.
The following points are helpful in constructing a frequency polygon:
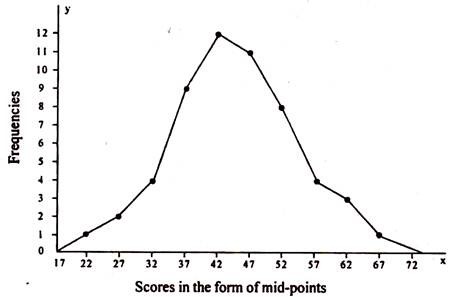 Figure 7: Frequency polygon of the frequency distribution given in table 2:
Figure 7: Frequency polygon of the frequency distribution given in table 2:
1. As in the histogram, two extra intervals or classes, one above and the other below the given intervals are taken.
2. The mid-points of all the classes (or intervals) including two extra intervals are calculated.
3. The mid-points are marked along the x-axis and the corresponding frequencies are plotted along the y-axis, by choosing suitable scales on both axies.
4. The various points obtained by plotting the mid-points and frequencies are joined by straight lines to give the frequency polygon.
5. For approximate height of the figure and selection of x and y units, the rule stated, in the case of histogram can be adopted.
Difference between a frequency polygon and a frequency curve:
(i) A polygon is a many-sided figure. It is essentially a closed curve while a frequency curve is not a closed curve.
(ii) In a frequency curve, we do not take two extra intervals or classes. But in a frequency polygon, we take these two extra classes in order to close the figure.
Comparison between the histogram and the frequency polygon:
Although both histogram and frequency polygon are used for the graphic representation of frequency distribution and are a like in many respects, they possess points of difference.
Some of these differences are cited below:
1. Where histogram is essentially the bar graph of the given frequency distribution, the frequency polygon is a line graph of this distribution.
2. In frequency polygon, we assume the frequencies to be concentrated at the mid-points of the class-intervals. It points out merely the graphical relationship between mid-points and frequencies and thus is unable to show the distribution of frequencies within each class interval. But the histogram gives a very clear as well as accurate picture of the relative proportions of frequency from interval to interval.
3. In comparing two or more distribution by plotting two or more graphs on the same axis, frequency polygon is more useful and practicable than the histogram.
4. In comparison to the histogram, frequency polygon gives a much better conception of the contours of the distribution, with a part of the polygon curve, it is easy to know the trend of the distribution but a histogram is unable to tell such a thing.
The Cumulative frequency Graph:
The data organised in the form of a cumulative frequency distribution may be graphically represented through the cumulative frequency graph (Fig. 8). It is essentially a line graph drawn on graph paper by plotting actual upper limits of the class intervals on the x-axis and the respective cumulative frequencies on the y-axis.
For the sake of better understanding, we can take the data given in Table 2:
Main points may be summarized in the following manner:
1. First of all we will calculate the actual upper limits of the class intervals as 24.., 29.5, 34.5, 44.5, 49.5, 54.5, 59.5, 64.5, 69.5, 74.5.
2. Then we will use the cumulative frequencies given next to the class intervals. In the case of a simple frequency distribution, table 2, the cumulative frequencies are first determined and written at the proper place against the respective class intervals.
3. Now, for plotting the actual upper limits of the class intervals on the x-axis and respective cumulative frequencies on the y-axis of the graph paper, we must select a suitable scale with reference to range of data to be plotted and the size of the graph paper to be used.
4. All the plotted points, representing the upper limits of the class interval with their respective cumulative frequencies, will then be joined through a successive chain of straight lines resulting in a line graph.
5. To plot the origin of the curve on the x-axis, it is customary to take one extra class-interval with zero cumulative frequency and thus calculate the actual upper limit of this class interval.
In the present case, the upper limit will be 19.5. It will be the starting point of the curve.
The Cumulative Percentage Frequency Curve or Ogive:
The cumulative percentage frequency curve (orogive) Fig. 9 is the graphical representation of a cumulative percentage frequency distribution such as given in Table 2. It is essentially a line graph drawn on a piece of graph paper by plotting actual upper limits of the class intervals on the x-axis and their respective cumulative percentage frequencies on the y-axis. Ogive differs from the cumulative frequency graph in the sense that here we plot cumulative percentage frequencies on the y-axis in place of cumulative frequencies.
The task of construction of this curve may be understood through the graphical representation in Fig.9 based on the data given in Table 2.
Use of the Cumulative percentage frequency curve or Ogive:
Cumulative percentage frequency curve (ogive) helps in the following tasks:
1. The statistics like median, quartiles, quartile deviations, deciles, percentiles and percentiles ranks may be determined quickly and fairly accurately.
2. Percentile norms (a type of noun representing the typical performance of some designated group/groups) may be easily and accurately determined.
3. We can have an overall comparison of two or more groups or frequency distributions by plotting the ogives concerning these distributions on the same co-ordinate axes.
Smoothing of frequency curves-polygon and ogive:
Why smooth:
Many times frequency curves obtained from some frequency distributions are so irregular and disproportionate that it becomes quite difficult to get some useful interpretations from them.
It usually happens in the situation when:
(а) The total number of frequencies (N) is small.
(b) The frequency distribution is somewhat irregular.
These irregularities in frequency distribution might have been minimized, if the data collected were numerous. In other words, there is a need for a fairly large sample to reduce the effect of sampling fluctuations upon frequencies in the classes.
Addition of cases on increase in the sample size irregularities. But if we cannot increase the size of the sample (where N is small) the kinks and irregularities in the frequency curves may only be removed by the process of smoothing the curve.
How to smooth:
One of the methods of smoothing a frequency distribution or curve is the method of “moving” or “running” averages.
The formula for this is as under:
Smoothed frequency of a class interval = 1/3 (frequency of given class interval + frequencies of two adjacent class intervals)
Let us show the computation of smoothed frequencies as given in Table 3:
Table 3:
Data for the computation of smoothed frequencies for polygon and ogive.
Explanation:
It is clear from table 3 that in the process of smoothing a curve (frequency polygon), we average actual frequencies, while in case of an ogive, the cumulative percentage frequencies are averaged.
For e.g., In case of frequency polygon, the smooth frequency related to the C.I. (55-59) is (4+3+7)/3 = 4.66 or 4.7 (app) while in case of ogive, the smooth cumulative percentage frequency related to this C.I. is (92+98+84)/3 = 91.33 or (91.3) app.
A slightly different procedure is to be adopted for calculating smooth frequencies for the class intervals at the extremes of the distributions.
For ex. the smooth freq. in case of polygon for class intervals 20-24 and 65-69 will be calculated as:
In the case of the ogive the smoothed cumulative percentage frequencies for these intervals are:
The smoothed frequency curves in the case of polygon and ogive for the data given in table 3 can be drawn in fig. 10 and fig. 11 respectively.